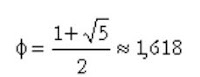Cours Théorie du Projet 3ème Année L.M.D - Département d’Architecture -Annaba-
Architecture et Géométrie : méthode géométrique
Le beau est ce qui par sa forme, ses proportions, ses raisons apporte une satisfaction dans l’appréciation esthétique : l’esthétique est la théorie et la connaissance du beau du point de vue du sentiment et de l’émotion, des idées et de la raison.
1- Proportion :
La proportion est le rapport harmonieux des parties entre elles et avec le tout.
Le tracé régulateur est la structure géométrique permettant la conception d’un plan.
Les anciens (Egyptiens, Grecs, Chaldéens,…) avaient déjà trouvés des systèmes de proportions basés sur les dimensions moyennes des éléments du corps humain de leur époque ; le pouce, le doigt, le pied, la foulée, la coudée, et s’en servaient pour construire leurs huttes, leurs maisons ou leurs temples.
Ils avaient déjà remarqué que, puisqu’une proportion exprimait l’égalité de deux rapports, trois termes au moins sont nécessaires pour écrire une proportion ; c’est le cas de la proportion continue en général, a/b =b/c, on peut essayer de simplifier encore et particulière, dans laquelle le troisième terme est la somme des deux autres, soit a/b = (a+b)/a, a étant le plus grand segment.
Cette proportion qui correspond donc à la coupe la plus simple d’une grandeur en deux parties inégales est appelée en géométrie élémentaire « partage en moyenne et extrême raison».
Exemple :
Sans appareil, un homme ne peut que comparer pour donner son jugement. Ce constat est d’une portée considérable, parfaitement illustrée par le problème classique de la corniche, tel qu’il est présenté par Georges Gromort(1) dans le chapitre qu’il consacre au « contraste » qui, selon lui, doit être le plus grand possible.
« D’une manière générale, un ensemble de moulures de ce genre comporte trois valeurs principales : les grandes telles que A, B, C, D, E ; celles de moyenne largeur, F, G, H ; enfin les moulures très fines, J, K. Il est visible qu’on s’est appliqué soigneusement à créer des contrastes partout. On remarquera que, presque jamais, deux moulures de même valeur ne se suivent ; deux moulures larges A et B (l’une d’ailleurs plate et l’autre de profil incurvé) sont séparées par un groupe J,G, dont l’ensemble lui-même est nettement moins fort que chacune des valeurs A et B. Mais dans ce petit groupe, le listel J et le talon G diffèrent encore (…) par leur degré de finesse … »(2)
(1) Gromort, Essai sur la théorie de l’architecture, 1937.
Pour obtenir le plus grand contraste possible, l’architecte ne peut pas accroître les différences entre les éléments. Il souhaite aussi que toutes les proportions soient estimables, inférieures au plus grand rapport estimable possible. Dès lors, dans une conception classique des proportions - qui va de 1,3 à 4 environ - il n’a pas à sa disposition plus de 3 à 4 grandeurs comparables deux par deux pour gérer les 10 éléments de sa corniche. Il range les éléments en classes contrastées, ABD, CE, FGH et JK, de telle manière que deux mesures quelconques soient toujours pratiquement égales, si elles appartiennent à la même classe, ou franchement différentes, si elles sont dans deux classes différentes. Par ailleurs, il fait en sorte que les mesures mitoyennes soient toujours contrastées : A # F & J, B # G & C, etc. Il cherche aussi à ce que les groupes d’éléments mitoyens soit, tantôt pratiquement égaux – EDKHC ≈ BGJAF – tantôt franchement différents - ED # KHC # B # GJAF.
L’extrême rareté des séries d’éléments qui peuvent être comparés deux par deux conduit les architectes à manipuler plusieurs séries distinctes et à clarifier les rapports entre les séries par des médiateurs. Dans une travée classique, par exemple, il n’y a pas de rapport estimable direct entre la colonne et l’entablement. En revanche, il y a des rapports estimables entre l’entablement (a), l’arc (b) et les piédroits (c). Il y a des rapports estimables entre l’entablement, les bases (f) et les chapiteaux (d,e). L’entablement a un rôle médiateur entre la série des grandes dimensions – arcs, piédroits, colonnes - et la série des petites dimensions – bases et chapiteaux.
2- L’être humaine et l’univers :
Le corps humain, avec ça hauteur, avec les dimensions de ses membres, l'écart de ses pas et ses possibilités de mouvements, constitue la mesure extérieure selon laquelle est jugée toute
architecture.
En recherchant des rapports entre Les différentes mesures des éléments du corps humains, ils définissaient des systèmes de proportions, et l’on peut dire que chaque époque était particulière, car des architectes essayaient d’améliorer ces systèmes de proportions pour les rendre adaptés à la culture et à la nouvelle vision du monde. Nous avons vu les plus connues, ce sont, le nombre d’or, la section dorée, le partage en moyenne et extrême raison.
Pour mieux illustrer le passage de rapports géométriques à des proportions humaines, il suffit de remarquer qu’il existe une certaine correspondance de proportion dorée entre la distance du sommet de la tête aux épaules, et la distance des épaules au nombril soit un rapport A.
D’autre part, entre la distance du sol aux genoux, et la distance des genoux au nombril; soit un rapport B. Et entre A et B on peut apercevoir un certain rapport dorée.
Au cours des siècles; nombreux sont les artistes ou les architectes qui ont travaillé à préciser d’anciens rapports ou à définir des nouveaux rapports. Nous citerons los plus célèbres DURER, ALBERTI, LEONAHD DE VINCI, MICHEL ANGE, ZEIZING, Il reprenait d’une manière plus contemporaine la série du « nombre d'or » développé par FIBONACCI
* (Le mathématicien FIBONACCI avait développé une série dimensionnelle partant de nombre entiers avec des rapports s’approchant du nombre d'or.
La série était généré (partant de deux fois le nombre 1, on pouvait trouvé la somme de deux nombres successifs.
1 ---------------1:1
1+1=2---------2 :3
1 + 2=3-------3:5
2+ 3=5--------5:8
3+5=8---------8:13
5+8=13-------13:21
8+13=21------21:34 …etc.
C’est le rapport connu sous le nom de « section dorée » ou « nombre d’or », lorsque ce rapport existe entre les deux parties d’un tout, il détermine entre le tout et ses parties une proportion telle que : « le rapport entre la plus grande des deux parties et la plus petite est égal au rapport entre le tout (la somme des deux grandeurs considérées et la plus grande ».
Quelles que soient les descendances pratiques et théoriques du module, elles n’ont plus, depuis longtemps, l’assise solide d’une référence religieuse. Dans la première moitié du 20e siècle, c’est en effet dans les avant-gardes que se niche le mysticisme des temps anciens.
Mais le goût des artistes a changé : ils juraient par les nombres entiers ; ils n’adorent plus que les nombres irrationnels, tout particulièrement la section d’or, «mythe moderne» qu’il va falloir désosser à la suite de Marguerite Neveux(1).*
Fibonacci dit Léonard de Pise (vers1175-1240), mathématicien, introduit en Occident les mathématiques arabes. Suite de Fibonacci : suite d'entiers dans laquelle chaque terme est égal à la somme des deux termes précédents soit 1, 2, 3, 5, 8, 13, 21, 34, 55, ... et dont le rapport de deux termes consécutifs tend vers Ø.
(1) Neveux, Le nombre d’or, radiographie d’un mythe, 1995.
Le nombre d’or est
C’est au début du XXe siècle que la section d’or apparaît dans le domaine des arts et de l’architecture.
Le Corbusier est un ardent promoteur de la «Divine Proportion». Il s’en fait le héraut dans «Vers une architecture». Il y mentionne deux types de rapports : le «lieu de l’angle droit», pour le capitole, le Petit Trianon, et la section d’or, qu’il utilise explicitement dans ses projets. Après ce qui est peut être la plus belle illustration des «tracés régulateurs» fondés sur un module, Le Corbusier s’en tient, en ce qui concerne la proportion, à marteler ce qu’il croit être une évidence : « le passé nous a légué des preuves.».
En 1945, Le Corbusier développait une nouvelle règle proportionnelle qui se nommait "Modulor". C’est avec «Le Modulor, essai sur une mesure harmonique à l’échelle humaine applicable universellement à l’architecture et à la mécanique» (1), que Le Corbusier va complètement théoriser ses rapports amoureux à 1,618. L’ouvrage émerge pendant la guerre. « … Tel est mon rêve. Prenez l’homme-le-bras-levé, 2,20 m de haut, installez-le dans deux carrés superposés de 1,10 m; faites jouer à cheval sur les deux carrés, un troisième carré qui doit vous fournir une solution. Le lieu de l’angle droit doit pouvoir vous aider à situer ce troisième carré. « Avec cette grille de chantier et réglée sur l’homme installé à l’intérieur, je suis persuadé que vous aboutirez à une série de mesures accordant la stature humaine (le bras levé) et la mathématique…arrivait une première proposition»(2)
Le Corbusier, ensemble de dimensions, Modulor
On a compris que le Modulor est d’abord une figure finie, un ensemble de dimensions (au sens propre, des proportions rapportées à un homme debout, bras levé) renvoyant à des pratiques : homme assis, attablé, debout, accoudé, etc.
(1) Le Corbusier, Le Modulor 1, 1950. Réed. Denoël, 1977.
(2) Idem.
Nous venons de voir qu’il doit exister des rapports de proportions harmoniques pour que la forme nous procure une satisfaction, mais elle doit aussi satisfaire la raison. Par exemple une porte même de proportion harmonieuse ne peut pas dépasser une mesure première qui lui est propre et qui est fonction du corps humain, et qui est deuxièmement fonction de la façade dans laquelle elle s’inscrit. Si on multiplie par dix ses dimensions, elle paraitra ridicule. Le schéma des ouvertures de portes proposées par Alberti lui-même : Les portes, nous dit-il, doivent être proportionnées aux façades, être plus hautes que larges," mais encore les plus hautes d'entres elles ne doivent excéder deux cercles l'un sur l'autre pris sur le diamètre du seuil & celles qui sont les plus basses, avoir en leurs côtés ou piedroits la hauteur diagonale qui se peut tirer d'un carré dont la ligne d'en bas fait la largeur de l'ouverture."
L'architecture et art de bien bastir, Leon Baptiste Alberti
Nous voyons là, l’importance de la raison et son origine, la relation fondamentale entre les proportions architecturales et le corps humain.
Tags:
C.theorier